Have you ever played a game of soccer, measured your weight, or watched a car race? If you have, you’ve dealt with scalars and vectors! Scalars and vectors are two types of quantities we use to describe the world around us. But what are they, and how do they work? Let’s find out!

What are Scalars?

Scalars are quantities that only have magnitude. Magnitude is just a fancy word for size or amount. Scalars tell us how much of something there is, but not in which direction. Think of it like this: if you ask your friend how much money they have, and they say “10 dollars,” that’s a scalar. You know the amount, but direction doesn’t matter here.

Examples of Scalars:

1. Temperature: When you say it’s 30 degrees Celsius outside, you’re using a scalar. You’re only telling the temperature, not the direction.
2. Weight: If you weigh 50 kilograms, that’s a scalar. It tells you how heavy something is, but not in which direction the weight is acting.
3. Speed: If a car is going at 60 kilometers per hour, it’s a scalar. It tells you how fast the car is moving, but not where it’s going.

Scalars are easy to understand because they only have one piece of information – the amount.

What are Vectors?

Vectors, on the other hand, have both magnitude and direction. This means they tell you how much of something there is and in which direction it’s going. Imagine pointing an arrow in a certain direction and then saying how long the arrow is – that’s a vector!

Examples of Vectors:

1. Displacement: If you walk 10 meters north, that’s a vector. It tells you how far you’ve walked (10 meters) and in which direction (north).
2. Velocity: If a car is moving at 60 kilometers per hour to the east, that’s a vector. It tells you the speed (60 kilometers per hour) and the direction (east).
3. Force: If you push a box with a force of 5 newtons to the right, that’s a vector. It tells you the strength of the push (5 newtons) and the direction (right).

Vectors are like giving directions with a map – you need to know both the distance and the direction to get to your destination.

Representation of Scalars and Vectors

Representation of Scalars: Scalars are simply represented by a number and a unit. For example:

• Temperature: 30 degrees Celsius
• Weight: 50 kilograms
• Speed: 60 kilometers per hour

Representation of Vectors: Vectors are represented by arrows. The length of the arrow shows the magnitude, and the direction of the arrow shows the direction. Here’s how you can represent vectors:

Science Notes

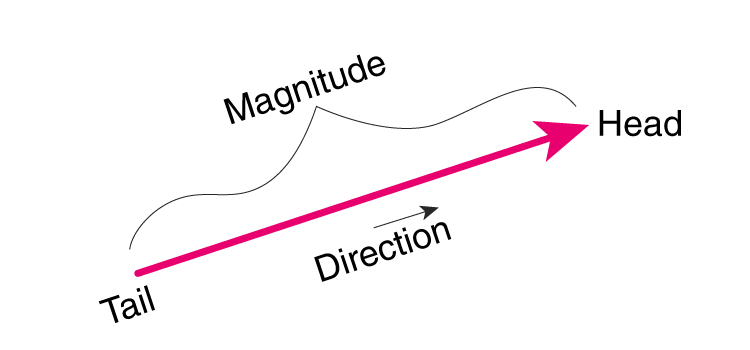
1. Graphically: Draw an arrow. The length of the arrow represents the magnitude, and the direction in which the arrow points represents the direction. For example, an arrow 5 cm long pointing east might represent a force of 5 newtons to the east.
2. Symbolically: Use symbols like → over letters. For example, vector A can be written as .
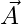3. Component Form: Break the vector into its horizontal (x) and vertical (y) components. For example, a vector 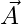might have components ​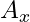 and ​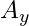, which tell you how much of the vector points in the x and y directions, respectively.

How Scalars and Vectors Work Together

Now that we know what scalars and vectors are, let’s see how they work in real life.

Example 1: Running a Race

Imagine you’re running a 100-meter race. The distance you run is a scalar because it only tells you how far you’ve run. But if you tell someone you ran 100 meters north, you’re using a vector because you’ve included the direction.

Example 2: Lifting Weights

When you lift a weight, the amount you lift is a scalar. But if you lift 10 kilograms upwards, you’re describing a vector because you’ve included the direction.

Example 3: Driving a Car

If you’re driving a car at 50 kilometers per hour, you’re describing a scalar. But if you’re driving 50 kilometers per hour to the east, you’re using a vector because you’ve included the direction.

How to Add Vectors

Sometimes, you need to add vectors together. For example, if you walk 3 meters east and then 4 meters north, you can’t just add the numbers together. You need to consider the direction too.

To add vectors, you can use a method called the tip-to-tail method. Here’s how it works:

1. Draw the first vector. For example, draw an arrow 3 meters long pointing east.
2. Draw the second vector starting from the tip of the first vector. For example, draw an arrow 4 meters long pointing north from the end of the first arrow.
3. Draw a new arrow from the start of the first vector to the tip of the second vector. This new arrow is the result of adding the two vectors together.

In this example, the new arrow would show that you’ve walked a total distance in a direction that’s a combination of east and north.

Scalars and Vectors in Everyday Life

Let’s look at more everyday examples to see how scalars and vectors are used.

Example 1: Grocery Shopping

When you carry a 5-kilogram bag of apples, you’re dealing with a scalar. The weight of the bag is a scalar quantity. But if you lift the bag upwards with a force of 5 newtons, you’re dealing with a vector.

Example 2: Traveling

When you travel to a new city, the distance you travel is a scalar. But if you say you traveled 200 kilometers north, you’re using a vector because you’ve included the direction.

Example 3: Playing Soccer

When you kick a soccer ball, the force of your kick is a vector. It has both magnitude (how hard you kick) and direction (where you aim the ball).

Difference between Scalars and Vectors

Feature	Scalars	Vectors
Definition	Physical quantities with magnitude only (no direction).	Physical quantities with magnitude and direction.
Representation	Usually represented by a single number or variable.	Represented by magnitude and direction (often denoted by an arrow).
Examples	Mass, temperature, time, speed, energy.	Displacement, velocity, acceleration, force.
Mathematical Operation	Scalars combine with scalars via simple arithmetic operations (addition, subtraction, multiplication, division).	Vectors combine with vectors via vector addition, subtraction, scalar multiplication, and vector multiplication (dot product, cross product).
Notation	Typically represented in italics (e.g., ( m ), ( T ), ( t )).	Often represented in bold or with an arrow (e.g., ( ), ( ), ( )).
Directionality	No inherent direction associated.	Has direction specified by its components or by an arrow pointing in the direction of the vector.

This table summarizes the key differences between scalars and vectors in terms of definition, representation, examples, mathematical operations, notation, and directionality.

Conclusion

Understanding scalars and vectors is like having a toolbox that helps you describe the world around you. Scalars tell you how much of something there is, while vectors tell you both how much and in which direction. Whether you’re running a race, lifting weights, or driving a car, you’re constantly using scalars and vectors without even realizing it.

So next time you play a game, do your homework, or just go about your day, remember that scalars and vectors are at work, helping you understand and navigate the world!